以梯度圖呈現三項連續變項的差異

發表於 更新於

本文簡介怎麼用 ggplot2 套件以下圖 B 的方式表示三項連續變數關係。

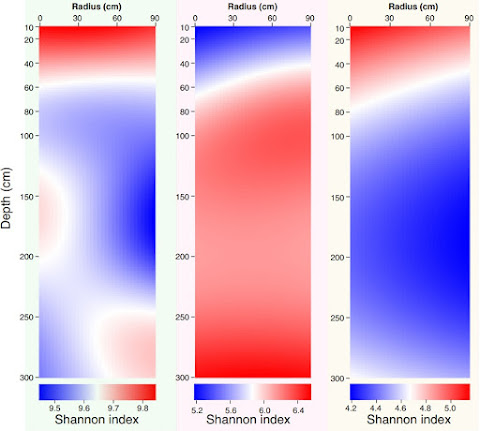
（Jiao et al. (2017) 利用這三張圖展示了林木周圍不同深度和半徑的土壤微生物多樣性變化。Jiao et al. (2017). Soil microbiomes with distinct assemblies through vertical soil profiles drive the cycling of multiple nutrients in reforested ecosystems. Microbiome.）

三項連續變數的資料視覺化

散點圖能清楚表達兩項連續變數的關係，若要新增第三項連續變數有以下策略：

  • 改變資料點的屬性以表示第三變數：這方法常用在類別變數或梯度明顯的連續變數。然而，我們對顏色、透明度、尺寸和形狀的變化不若位置敏感，如果資料充滿雜訊或趨勢不明顯，基於原始資料的圖表將不易解讀。
  • 將連續變數切割為類別變數：雖然類別變數較容易視覺化，但是切割可能引進選擇偏誤，也會損失部分的資訊。
  • 繪製三維圖表：為了在平面上展示三維圖表，原始資料在映射至三維空間之後，得投影到平面上才能呈現。因此，三維圖表雖然能同時展示三種變數，但資料點之間的關係也因為二重轉換而扭曲。三維圖表造成混淆的案例可參考 Don’t go 3D, Fundamentals of Data Visualization.Claus O. Wilke. ）
  • 將各變數兩兩一組繪製二維圖表：雖然此舉能保留全數資訊，但沒辦法同時比較三項變數的關係。

除了三維圖表會扭曲資料外，其它策略都能忠實反映原始資料中三項連續變數的關係。因此真正的問題在於，如果資料充滿雜訊或趨勢隱晦的時候，應該用原始資料配合哪種圖表才能支持自己的主張？

以梯度圖展示三項連續變數的關係

現在回到本文開頭的那張梯度圖，仔細看可以發現圖中每個位置都有相應的 shannon 多樣性數值。由於正常採樣不可能達到如此完整的覆蓋率，所以這張圖展示的其實不是原始數據，而是為了支持作圖者觀點，基於原始數據建模後得出的預測值。

雖然第一次看到可能不易聯想到這層關係，但這種做法在兩項連續變數的資料視覺化相當普及。例如我們可用年齡為橫軸，腸道微生物多樣性為縱軸，作散佈圖檢視兩者的關聯。接著依照資料點的分布，適配不同的迴歸模型以描述多樣性逐年齡變化的趨勢。

換句話說，梯度圖的顏色等同於散佈圖的迴歸曲線，儘管呈現的不是原始資料，但能輔助讀者判斷趨勢的模型預測值。


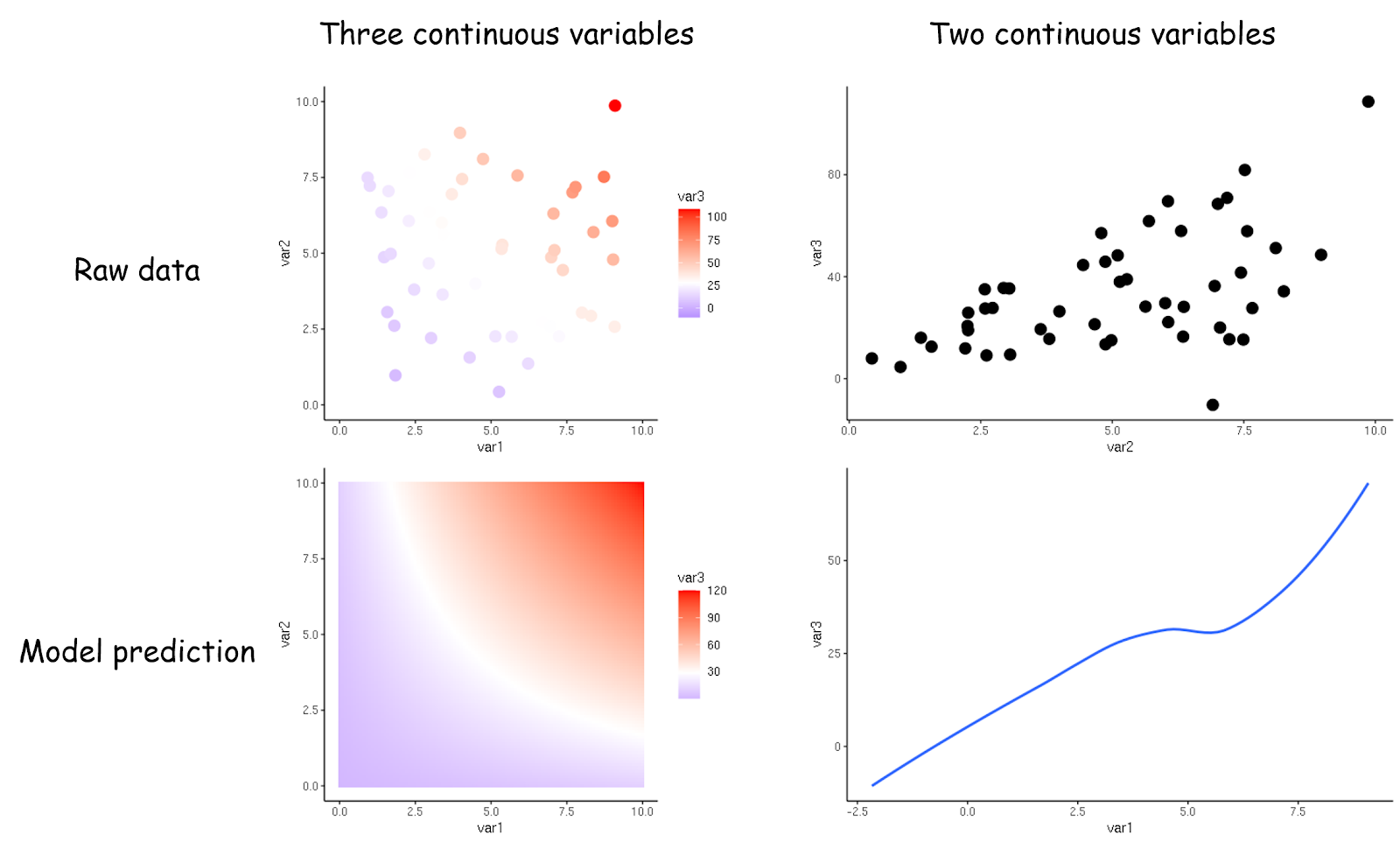
（梯度圖的顏色等同於散佈圖的迴歸曲線，是輔助讀者判斷趨勢的預測值。）

以 ggplot2 實作梯度圖

繪製梯度圖的方法可參考這則貼文（https://stackoverflow.com/questions/41988812/plot-smoothed-average-of-third-variable-by-x-and-y）

首先從常態分佈（平均值 = 5，標準差 = 2.5）隨機抽樣 50 對數值組成模擬資料的變數一 (var1) 和變數二 (var2)，再將變數和加上變數積形成變數三 (var3)。

1
2
3
data <- data.frame("var1" = rnorm(50, mean = 5, sd = 2.5), 
                   "var2" =rnorm(50, mean = 5, 2.5))
data$var3 <- data$var1 + data$var2 + data$var1*data$var2

接著，用模擬資料建立預測模型以 var1 和 var2 預測 var3。由於目的是呈現變數間的關係，而不是評估各項變數對於預測值的貢獻度，所以採用局部迴歸演算法以呈現資料的特性。

1
2
3
ml <-  loess(var3 ~ var1 + var2, 
             control = loess.control(surface = "direct"), 
             data = data)

模型完成後，新增一張包含 var1、var2 以及預測值（var3）的資料表。這張資料表將用於繪製梯度圖，因此圖表兩軸的刻度應視 var1 和 var2 的尺度調整。

1
2
3
df  <-  expand.grid("var1" = seq(0, 10, by = 0.1), 
                    "var2" = seq(0, 10, by = 0.1))
df$var3 <- c(predict(ml, newdata = df, type = "response"))

最後使用磚瓦圖，基於新資料表繪製梯度圖。在此圖中，將 var3 的中位數作為顏色變化的中間點，以彰顯 var3 的梯度變化。

1
2
3
4
5
6
7
8
9
ggplot(data = df) +
  geom_tile(mapping = aes(fill = var3,
                          x = var1,
                          y = var2)) +
  scale_fill_gradient2(low = "blue",
                       high = "red", 
                       midpoint = median(df$var3)) +
  coord_fixed(ratio = 1, xlim = c(0, 10), ylim = c(0, 10)) +
  theme_classic()


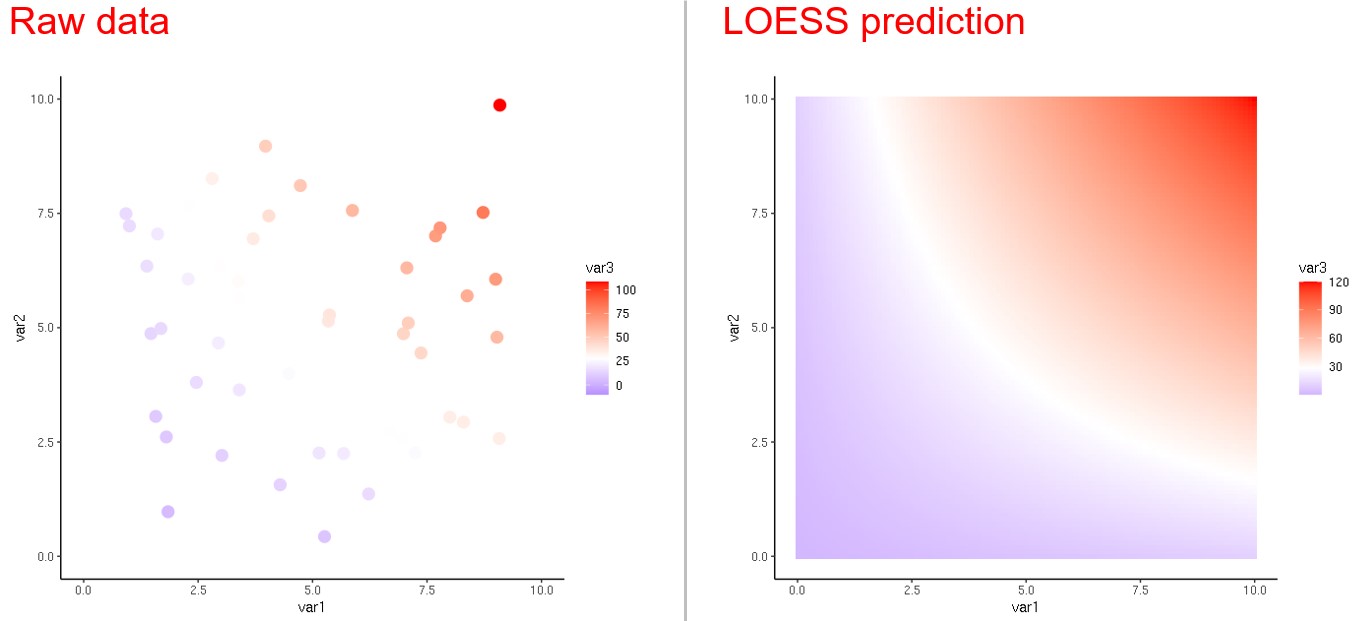
（建模時可以有假設和推論，但要誠實揭示原始資料以免誤導讀者）

結論

改變資料點的屬性、轉換連續變數轉換為類別變數或將各變數兩兩一組製成二維圖表是呈現三項連續變數關係的常見策略，然而當資料充滿雜訊或趨勢隱晦的時候，可以用梯度圖輔助讀者判斷趨勢。由於梯度圖是支持作圖者主張的模型，所以仍需揭露原始數據供讀者參考，以免誤導之嫌。