如何界定細菌性狀預測演算法的有效範圍？

hidden state prediction (HSP) 是一種基於分子演化關係來預測未知基因功能的演算法 (Zaneveld & Thurber, 2014)，它能用於重度仰賴定序技術的微生物生態研究，提供性狀或功能面的資訊 (Guittar et al., 2019)。

儘管存在這樣有力的生態學研究工具，卻還沒有統一的方式來驗證其有效範圍。在應用 HSP 的研究中，Guittar et al. (2019) 沒有考量預測誤差，Langille et al. (2013) 沒有界定適用範圍。因此，我想以他們的研究為基礎，設計能評估預測工具有效範圍的方法。

使用 HSP 需要準備譜系樹和性狀註解。以下圖為例，枝頭上的數字表示某種性狀的數值，標示問號的方格表示未知性狀的基因。HSP 能透過其他數值已知而且親緣關係相近的基因來推論其數值。

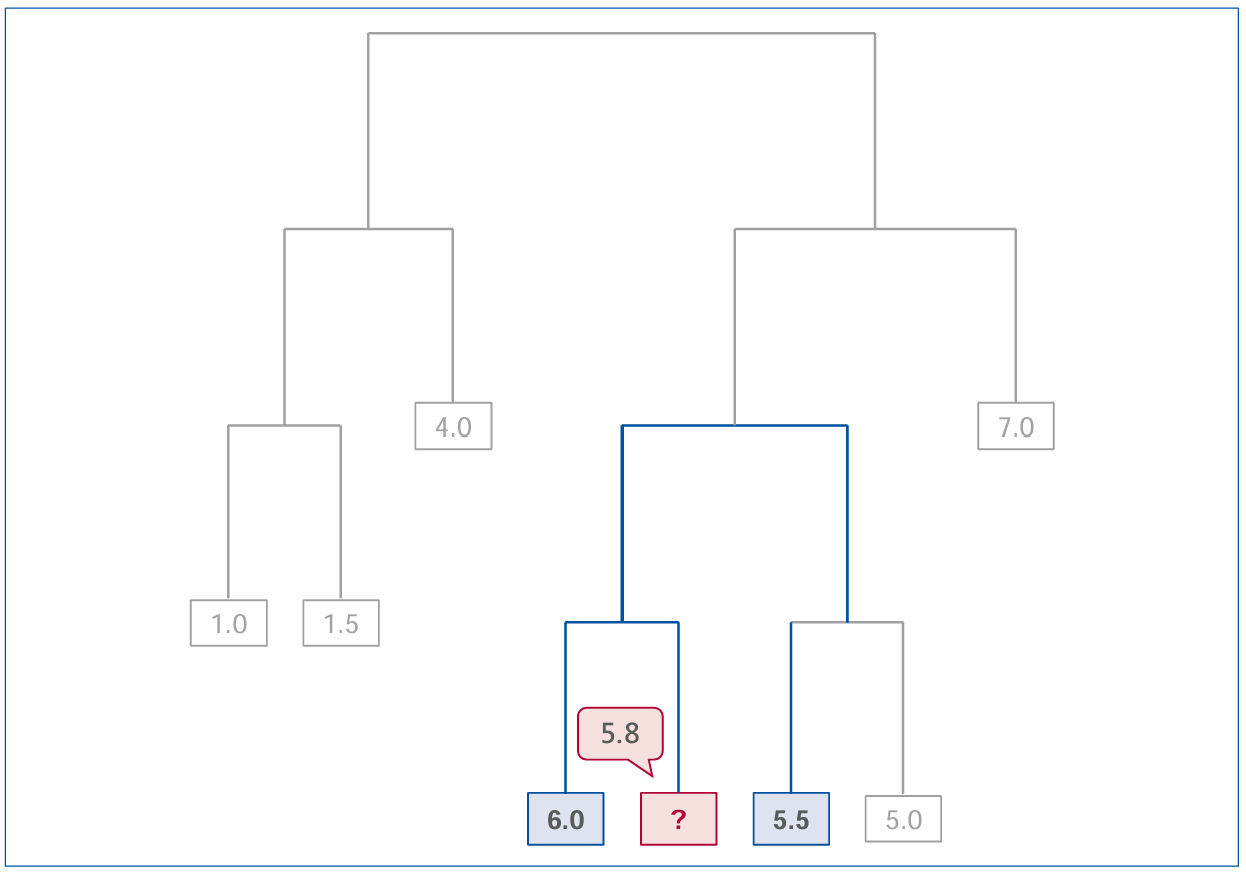
雖然我未必掌握了 HSP 的運算細節，還是能利用基本原則：預測的準確度會隨可利用的資訊遞減。如果未知性狀的基因和其他枝頭的親緣關係很遠，那麼預測的效度應該也不會太好。基於這種原則，我們可以把 HSP 當作一個黑箱，利用既存的譜系樹來了解預測能力和既有資訊的關係。

首先，我先指定一個已知性狀的基因，再由近到遠逐步移除親緣關係相近的基因。每次移除資料，都使用 HSP 預測指定基因的性狀值，並且計算預測值與觀察值的差異，取得預測誤差和資訊量的關係。

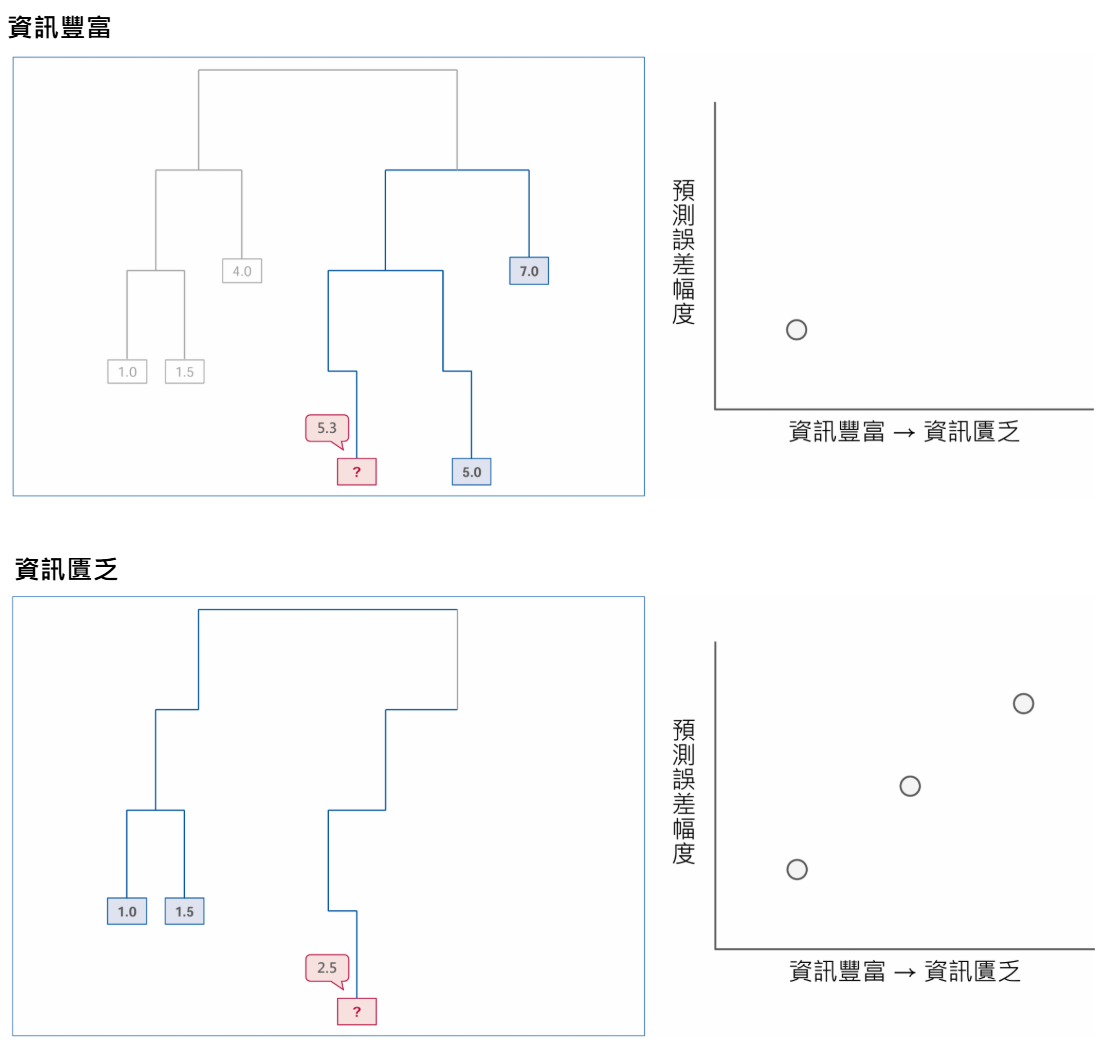
原則上，資訊損失量與預測誤差為正相關，而這關係的模式可能是線性、指數成長或是邏輯式分布等，可以建置對應的方程式來描述兩者的關係。接著，比較演算法預測與隨機預測的誤差值，兩條線交點的截距，即是預測演算法的有效範圍，在這範圍以內，演算法都優於隨機猜測。隨機猜測的方式可以任意挑選兩個節點為代表。

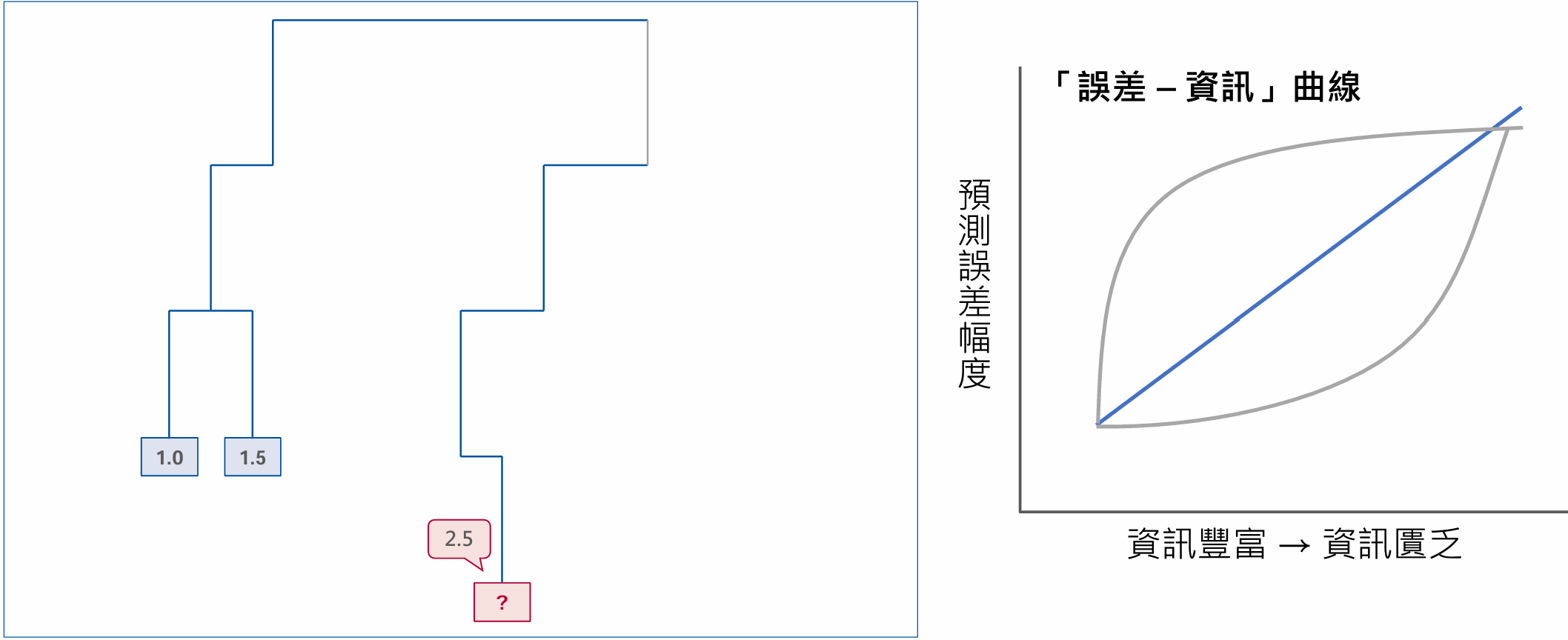
例如下圖左邊的示範資料中，我發現預測錯誤率和資訊量呈線性關係，再比較隨機預測的誤差，便能得到一個範圍，當資訊量在範圍之內時，可以確保演算法的預測比隨機猜測可靠。

---

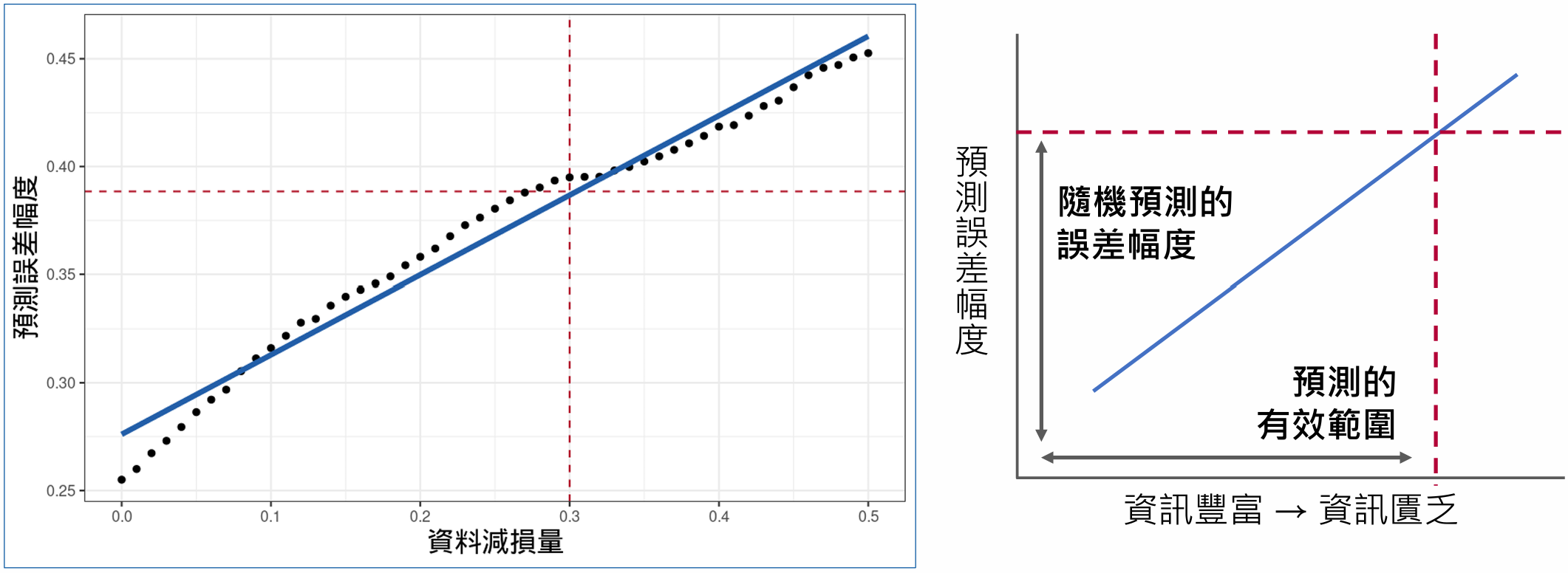
Guittar et al. (2019). Trait-based community assembly and succession of the infant gut microbiome. Nature communications, 10(1), 1-11.

Langille et al. (2013). Predictive functional profiling of microbial communities using 16S rRNA marker gene sequences. Nature biotechnology, 31(9), 814-821.

Zaneveld & Thurber. (2014). Hidden state prediction: a modification of classic ancestral state reconstruction algorithms helps unravel complex symbioses. Frontiers in microbiology, 5, 431.