ROSALIND｜Building a Heap (hea)

發表於 更新於

給定長度為 n 的整數數列，將其轉置為二元最大堆 (binary max heap)。

Given: A positive integer $n \leq 10^5$ and array $A[1..n]$ of integers from $-10^5$ to $10^5$.

Return: A permuted array $A$ satisfying the binary max heap property: for any $2 \leq i \leq n$, $A[\lfloor i/2 \rfloor] \geq A[i]$.

(https://rosalind.info/problems/hea/)

背景知識

樹 (tree) 是由節點 (node) 連結而成的階層式資料結構，其形態與自然界的樹木相仿，由單一節點延伸數條分支，當中不存在環狀結構。樹的每個節點能延伸出多個子節點 (child node)，但只能源於一個親節點 (parent node)，來自相同親節點者互為平輩 (siblings)。沒有親節點者稱為根 (root)，沒有子節點者則為葉 (leaf)，由根走向特定節點所經歷的節點數即為該節點所在的層數 (level) 或深度 (depth)。

二元樹 (binary tree) 是各節點最多有兩個子節點的樹，可以明確定義出樹的輪廓（即層數、節點數等特性）。因此，相較於其它種樹，二元樹具有次序性，會因為節點的排列順序而異。

1
2
3
  P          P
 / \   !=   / \
L   R      R   L

二元樹依照子節點的填滿程度和順序可分為以下幾類，

  • 完滿二元樹 (full binary tree)：除了葉節點，各節點皆恰好有兩個子節點的二元樹。
  • 完美二元樹 (pefect binary tree)：所有葉節點皆位於同一層的完滿二元樹。
  • 完全二元樹 (complete binary tree)：除了最底層，其餘層皆填滿；最底層的節點由左至右連續排列沒有空隙。


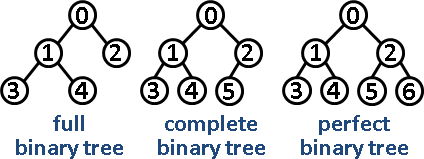
（二元樹的種類。圖/演算法筆記）

完全二元樹的節點能由左至右、由上至下填入一維陣列中。假設陣列的索引從 0 開始，則任意節點 X 在陣列中的位置 $i$ 可表示為：

$$2^L - 1 + n$$

其中，$L$ 為節點 X 所在的層數（由 0 開始計數，根節點為第 0 層），$n$ 為節點 X 在該層的順序（由左至右從 0 開始計數）。舉例來說，下圖的節點 5 位於第 2 層，是該層第 2 個節點，因此位置為 $2^2 - 1 + 2 = 5$

這個公式的原理是，節點在陣列中的位置相當於前面所有層的節點總數，加上節點在該層的次序。對於第 $L$ 層的節點，在它之前的節點總數為 $2^0 + 2^1 + 2^2 + … + 2^{L-1}$，此級數可化約為 $2^L - 1$，再加上節點在當前層的位置 $n$，即可得出前述公式。

1
2
3
4
5
6
7
8
9
10
11
# tree view
     0        lv 0 (#nodes: 2^0)
    / \ 
  1     2     lv 1 (#nodes: 2^1)
 / \   / \
3   4 5   6   lv 2 (#nodes: 2^2)

# array view
[ 0   1   2   3   4   5   6  ]
 └─┘ └─────┘ └──────────────┘
 lv0   lv1         lv2

基於陣列的表示法，可以進一步推導與 X 相連之其它節點的位置公式。

  • 親節點：$\lfloor (i-1)/2 \rfloor$
  • 左子節點：$2i + 1$
  • 右子節點：$2i + 2$

這裡以右子節點的推導為例說明這些公式的來歷。考慮位於第 $L$ 層第 $n$ 個節點 X，它的右子節點會在下一層 $L+1$。因為每個節點都有兩個子節點，所以右子節點在第 $L+1$ 層的位置，相當於節點 X 之前所有節點產生的子節點總數，再加上節點 X 本身的左子節點，即 $2n + 1 = 2 (n + 1) - 1$。因為位置從 0 開始計數，所以這個數值正好等於右子節點在 $L+1$ 層的位置。

  • 右子節點之前所有層的節點總數：$2^{L + 1} - 1$
  • 右子節點在當層的順序：$2 (n + 1) - 1$

兩者之和為右子節點的位置：

$$2^{L + 1} - 1 + 2 (n + 1) - 1 = 2 (2^L + n - 1) + 2 = 2i + 1$$

基於同樣的推導方式，位於右子節點旁邊的左子節點位置為 $2i + 1 = 2i + 2 - 1$，而親節點的位置則可透過將子節點的位置除以二並無條件捨去來取得 $\lfloor (2i + 2)/2 \rfloor = i$。

解題觀念

此題要求我們將整數數列轉換為 binary max heap。Heap（堆）是特殊的完全二元樹，它的親子節點具有一致的次序關係。舉例來說，max heap 的親節點恆大於子節點，heap 的最大值位於根節點。反之，min heap 的親節點恆小於親節點，根節點存放 heap 的最小值。

構建 heap 有 William’s method 和 Floyd’s method 兩種截然不同的策略。前者從無到有逐步建立，後者則將既有的樹重新整理。

William’s method

William’s method 可能是當中較為直觀的作法，它從一個空的完全二元樹開始，逐一添加新的節點，直到建立完整的 heap。

為了確保這棵完全二元樹滿足 heap 的特性，新的節點一開始會放置在樹的最後一個位置，然後與其親節點比較。若新節點大於親節點，兩者互換位置。重複這個過程，直到新節點攀升到它正確的位置上，亦即它的大小正好介於自己的親節點與子節點之間。每個新節點至多向上攀升 $log n$ 層，共有 n 個節點要添加，兩者相乘為 $O(nlog n)$ 的時間複雜度。

在樹的最末端添加新節點 比較新節點與親節點 向上移動到正確位置

（以 Williams’ method 構建 heap。圖/維基百科）

1
2
3
4
5
6
7
8
9
10
def hea(l):
    heap = [] # 準備一個空的完全二元樹
    for i, num in enumerate(l):
        heap.append(num) # 添加新節點到樹的最後一個位置
        parent = (i - 1) // 2
        while i > 0 and heap[i] > heap[parent]: # 比較新節點與親節點
            heap[i], heap[parent] = heap[parent], heap[i]
            i = parent # 更新新節點當前位置
            parent = (i - 1) // 2 # 下一個要比較的親節點
    return heap

親節點與其中一側的子節點交換並不會影響另一側子樹的結構。以下圖為例，5 為親節點，1 是左子節點，X 則是新加入的右子節點。如果 X > 5，兩者互換不會影響左子節點與 X 的關係，因為 1 本來就比 5 小，也自然會比 X 更小。這就是為什麼添加新節點並一路更新其位置的時候，不會破壞其它子樹的 heap 特性。

1
2
3
  5
 / \
1   X

Floyd’s method

Floyd’s method 則是將任意完全二元樹整理成 heap，不需要額外的儲存空間。這方法從最後一個非葉節點開始，假如這個節點小於它的子節點，則兩者互換位置，再從新位置持續向下調整，直到節點落到正確的位置上。重複著個過程，直到所有非葉節點都調整過後，即完成 heap 整理。

這個過程與 William’s method 相反，親節點是由上往下一路沉降到它應該存在的地方，每一次交換位置都不會影響另一側子樹的結構。被交換一側的子樹可能暫時違反 heap 的性質，但是持續向下更新的過程會將其調整回來。這也是為什麼 Floyd’s method 要從最後一個非葉節點開始處理，這樣才能確保當前節點的左右子節點都滿足 heap 性質。

（以 Floyd’s method 構建 heap。圖/維基百科）
如果一開始就從根節點更新，只有途經的節點會滿足 heap 的順序，其它節點則無法保證。舉例來說，從下圖的根節點 3 開始，會沿著左側子樹 3 -> 5 -> 4 的路徑更新位置，無法顧及右側的狀況，所以還得回頭檢查。

1
2
3
4
5
     3
   /   \
  5     1
 / \   / \
0   4 2   6

Floyd’s method 的時間複雜度為 $O(n)$，詳情參考維基百科 binary heap。簡言之，最差的情況就是要把一棵 min heap 轉置成 max heap。底層節點多，但是沉降的距離短；頂層的沉降距離長，但是節點少。兩相抵銷之後，最終效率會比 William’s method 還要高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def sift_down(l, i):
    n = len(l)
    # 確認親節點、左子節點、右子節點何者最大
    candidates = [idx for idx in [i, 2 * i + 1, 2 * i + 2] if idx < n]
    largest = max(candidates, key=lambda idx: l[idx])
    if largest != i:
        # 向下更新親節點的位置
        l[i], l[largest] = l[largest], l[i]
        return sift_down(l, largest)
    return l
def hea(l):
  # 檢查所有的非葉節點
  for i in range(len(l) // 2, -1, -1):
      l = sift_down(l, i)
      return l